Für diese Variante gibt es zwei alternative Implementierungsmethoden. Der rechenzeit-optimierte Algorithmus basiert auf der in Spiess & Florian (1989) beschriebenen Berechnung. Bei diesem Algorithmus können nur einfache Koordinierungen und additive Fahrpreise berücksichtigt werden. Der alternative Algorithmus erlaubt weitere Einstellungen für die Wahlmodelle und komplexere Definitionen bei Koordinierungen und der Berücksichtigung von Fahrpreisen. Beide Verfahren werden angewendet, wenn Sie Im Wahlmodell Fahrgastinformation Keine (Optimal Strategies) auswählen. Den rechenzeitoptimierten Algorithmus wählen Sie mit der entsprechenden Schaltfläche darunter.
Wenn der Fahrgast über keine zusätzlichen Informationen verfügt, ist er darauf angewiesen, beim Eintreffen einer Linie ad hoc zu entscheiden, ob er einsteigt oder nicht. Das Wahlmodell ermittelt die optimale Linienmenge, und die optimale Strategie des Fahrgasts besteht darin, die erste eintreffende Linie aus dieser Menge zu wählen.
Dieses Modell ist neben dem Fehlen von Fahrgastinformation vor allem dadurch gekennzeichnet, dass die Fahrzeugfolgezeit (der Abstand zwischen zwei Abfahrten einer Linie) nicht als konstant, sondern als exponential verteilt angenommen wird. Der Erwartungswert für diesen Abstand beträgt genau wie bei konstanten Takten 1 / λi, also die „Frequenz” der Linie. Im Unterschied zu konstanten Takten streuen die Fahrzeugfolgezeiten jedoch stark um diesen Wert.
Wesentliche Eigenschaft der hier zugrunde liegenden Exponentialverteilung ist, dass die bereits verstrichene Wartezeit seit der letzten Abfahrt auf der Linie nichts darüber aussagt, wie lange die Fahrgäste noch bis zur nächsten Abfahrt warten müssen. Diese Eigenschaft wird „Gedächtnislosigkeit” genannt. Es wird somit die größtmögliche Unregelmäßigkeit des Fahrplans unterstellt.
Die unter diesen Modellannahmen optimale Menge bildet man wie folgt. Zuerst setzt man Folgendes:
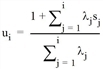
Dann erhält man die optimale Linienmenge durch L* = Li*, wobei i* = max{i:si≤ ui-1}.
Man kann zeigen, dass das so gebildete i* die erwarteten Restkosten minimiert.
Somit gehört eine Linie i genau dann zur optimalen Menge, wenn ihre Rest-Reisezeit (ohne Wartezeit) nicht höher ist als die erwartete Rest-Reisezeit plus Wartezeit der kombinierten Linien Li-1 = {1, ..., i-1}. Diese Vorgehensweise bewirkt, dass nur relativ wenige Linien benutzt werden, denn bei diesem Vergleich werden die Linien Li-1 so behandelt, als seien sie perfekt koordiniert. Koordiniert bedeutet hier, dass sie so gleichmäßig angeordnet sind, dass sie sich gemeinsam so darstellen wie eine einzige Linie mit Frequenz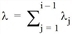 
. Eine solche Additivität ist nur bei exponentieller Verteilung gegeben.
Die Anteile der Linien i ∈ L* sind gleich der Wahrscheinlichkeit, dass sie als erste abfahren, wie folgender Formel zu entnehmen ist.
Es sollte beachtet werden, dass die Rest-Reisezeiten der Linien nicht in der Anteilsdefinition auftauchen. Wenn Linien hinreichend gut sind, um in der optimalen Linienmenge enthalten zu sein, hängt ihr Anteil nur noch von ihrem Takt ab. Diese Eigenschaft verdeutlicht die stark vereinfachte Konstruktion dieses Wahlmodells.
Die resultierende erwartete Wartezeit ergibt sich wie folgt.
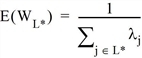
Sie sollten dieses Wahlmodell nur verwenden, wenn die Fahrzeugfolgezeiten der Linien extrem unregelmäßig sind, sich die Fahrgäste also einem sehr hohen Maß an Unsicherheit gegenüber sehen.
